正規分布とは?その2(標準誤差について)
本記事では下記を説明します。なお、分布について理解する必要があるので、1つ前の記事を事前にご覧ください。
- 正規分布はなぜ統計学で最重要と言われるか
- 標準誤差(Standard Error: SE)について
記述統計と推測統計
研究を行う場合、注目している全ての患者のデータを集めることは、コストや期間、倫理的理由などの様々な制約を考えると、一般的に不可能です。そのため、一部の患者を集めて研究を行います。注目している全ての患者が含まれる集団を母集団と言い、研究で集められた母集団の一部である集団を標本集団と言います。下図にイメージを示しました。
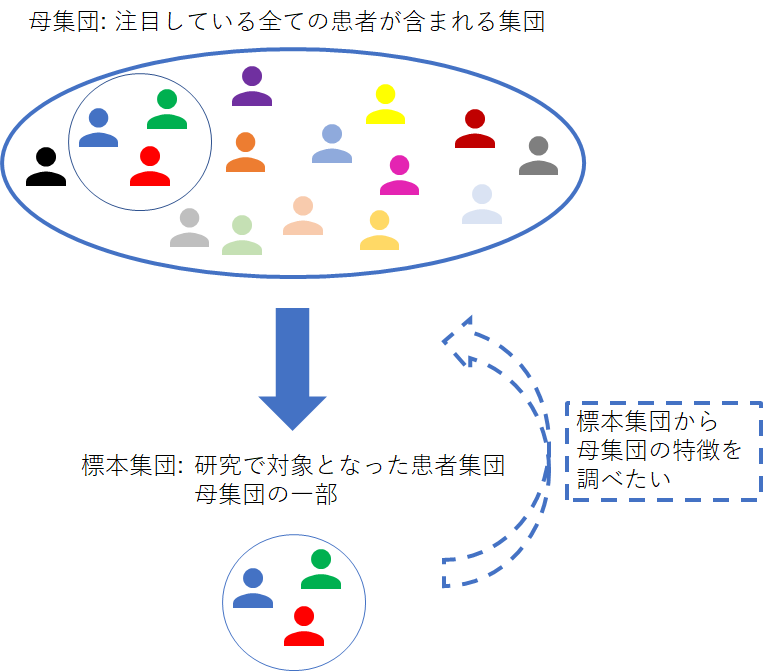
標本集団自体の特徴を要約するのが記述統計で、その名の通り集団の記述を目的とします。これは、1つ前の記事で示したように、標本集団を平均値と標準偏差(Standard Deviation: SD)で要約したり、ヒストグラムで要約したりという感じです。なお、日本国民全体に対して行われる全数調査の国勢調査は、その調査時点における日本国民全体という母集団データを得ているので、母集団の記述(平均値とSDで要約したり、ヒストグラムで要約したりという意味)が行われています。
しかし、標本集団の記述がメインの目的になることはほとんどなく、通常は母集団の特徴(母集団の平均値など)を調べることがメインの目的となります。標本集団から母集団の特徴を調べるのが推測統計ですが、本記事ではSEを説明します。
標本集団の平均値はバラつく
さて、SEを理解するために、まずは神様になりましょう。神様になるとは、以下の意味です。
- あなたは何度でも(過去に戻るなどして)研究を行えます
- あなたは母集団の特徴(母集団の平均値など)を知っています
仮にあなたが神様なら、母集団を知っているのですから、わざわざ研究を行う必要はありません。しかし、ここではSEを学ぶために、あえて研究を行うこととします。あなたが神様になったとして、何度も研究を行ったイメージが下図です。身長のデータを考えます。なお、個々の研究で集める患者の人数は一定(例えば100人)とします。
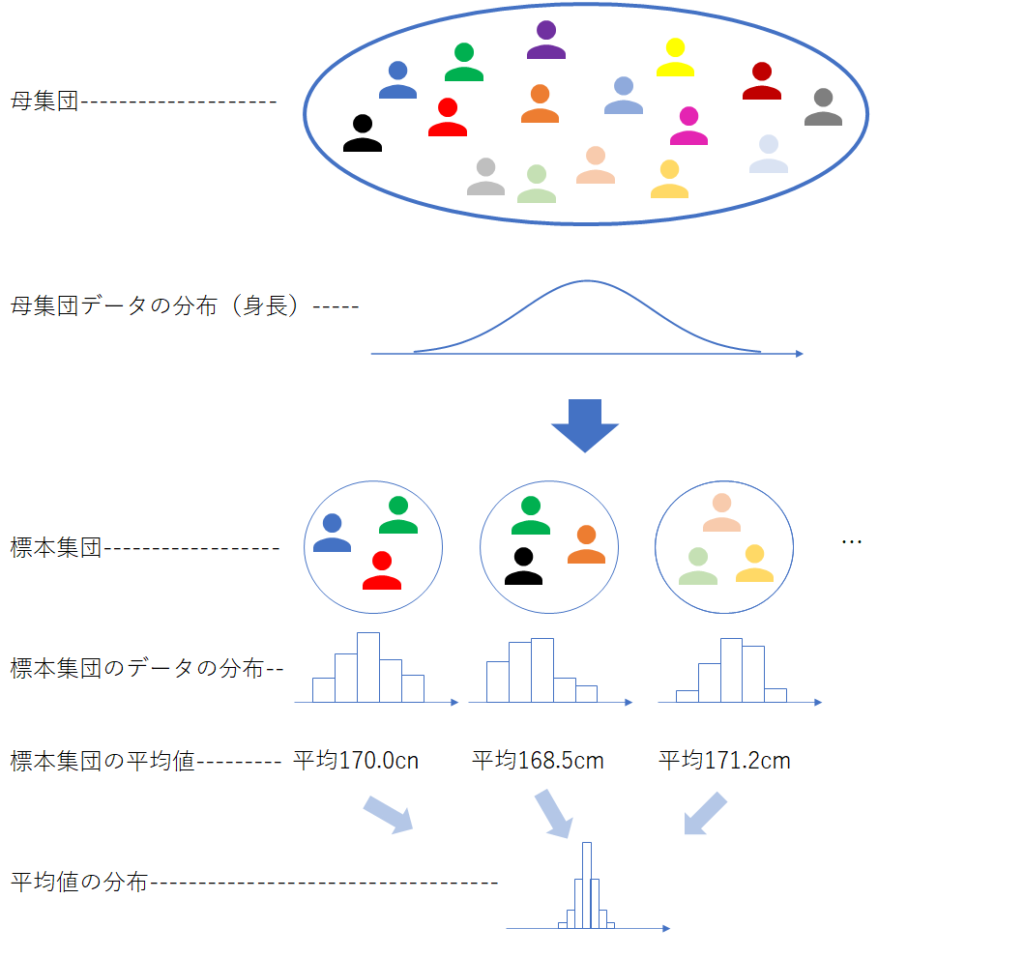
研究を繰り返すと、研究ごとに標本集団が得られます(複数の研究に同じ患者が含まれることもあります)。そうしますと、「平均値がいくつも得られる」ということが分かります。この「いくつも得られた平均値」のヒストグラム(平均値の分布)が上図の一番下になります。
さて、ここで「いや、でもそもそも実際には神様になれないじゃないか」という疑問が出てきますが、この後説明しますので、まずは「仮に神様になれたら」と思ってお読みください。神様になれれば、「標本集団の平均値はバラつく」ということが分かります。
データのバラつき(=SD)と平均値のバラつき(=SE)
さて、先ほどの例で「標本集団の平均値はバラつく」ことが分かりましたが、この平均値の分布に関して重要な事実があります。それを視覚的に確認するため、「サイコロの目の平均値の分布」を見てみましょう。ここでも神様になりましょう。
- あなたは何度でも研究を行えます(=「サイコロを振る作業を繰り返す」を何度でも行える)
- あなたは母集団の特徴を知っています(=1~6のサイコロの目が出る確率はそれぞれ1/6、平均値は3.5)
データを1つ得ることと、サイコロを1回振って目を記録することは同じです。また、ここでの母集団(サイコロを振るということに対応した母集団)をイメージしにくい方は、下記のように考えるとよいです。
ツボの中に、既に目が決まったサイコロが1~6の目で同じ数だけ無限に入っています。ツボからサイコロを取り出して目を記録してツボに戻すとします。そうすると、1~6の目を取り出す確率はそれぞれ1/6になります。このツボのイメージが母集団になります。このように、具体的な母集団(例えば先ほどの患者集団)ではなく、抽象的な母集団を考えることもできます。
さて、「サイコロを1、10、100、1000回振るごとに平均値を求める」を繰り返した時、サイコロの目の平均値の分布は下図のようになります。詳しいことは割愛しますが、これはコンピュータを用いて作成することができます。なお、先ほども述べましたが、標本集団のデータ数はサイコロを振った数となります。例えば、「サイコロを100回振るごとに平均値を求める」という場合、標本集団のデータ数は100、標本集団ごとに100のデータから1つの平均値が計算されます。
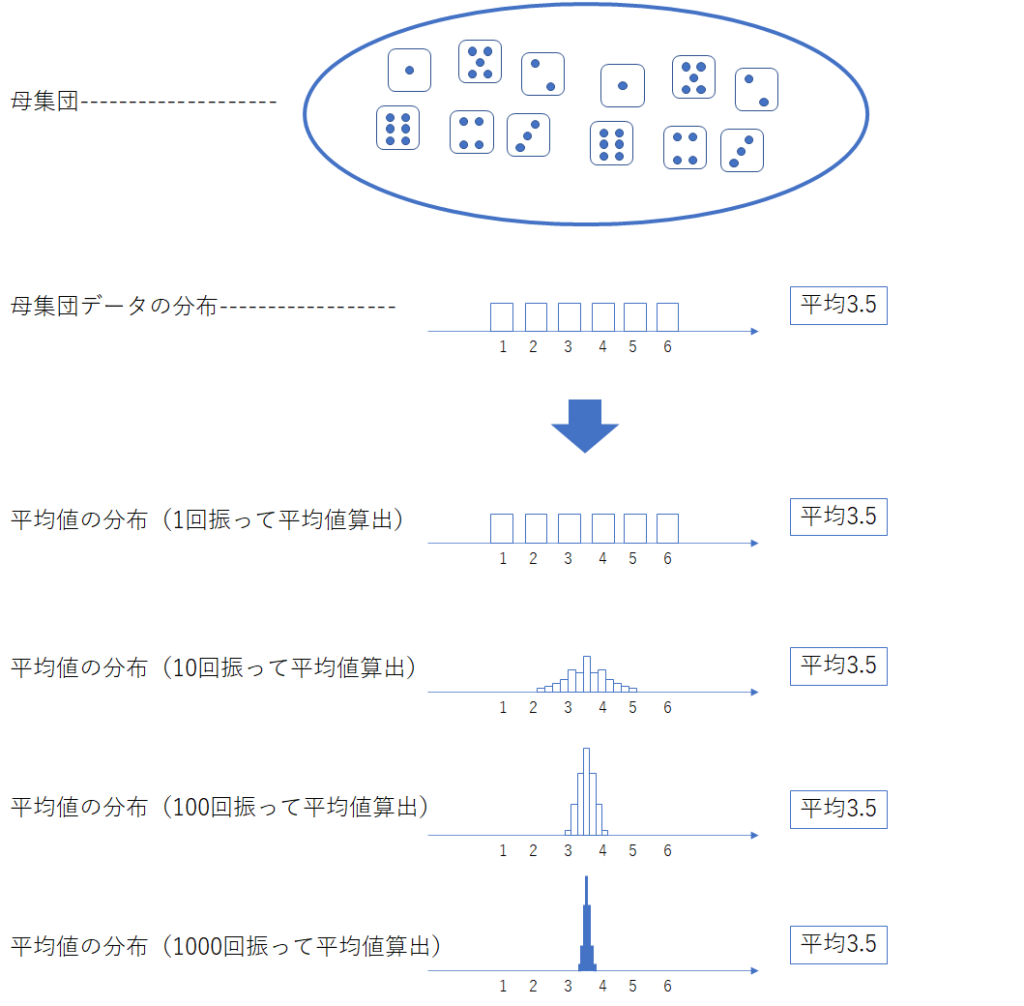
なんと!平均値の分布はデータ数を増やしていくにつれて、母集団データの分布からは似ても似つかない形となりました(実はこの形は正規分布です)。ここから、下記のことが分かります。
- 母集団データの分布が何であれ、平均値の分布は標本集団のデータ数が増えると正規分布に近づく
- 平均値の分布の平均値は、母集団データの平均値に一致する
- 平均値の分布のバラつきは、標本集団のデータ数が増えると小さくなる(平均値の分布の山が鋭くなる)
3については、理論的に下記の関係があります。なお、数式は理解できなくても構いません。言葉で説明している部分を理解できれば十分です。
$$SE=平均値の分布のSD=\frac{母集団データの分布のSD}{\sqrt{標本集団のデータ数}}$$
上の式の中で、「母集団データの分布のSD」というものは実際には神様でないと分かりません。そこで、これを「標本集団データの分布のSD」で置き換えたものをSEとします。それが下記です。
$$SE=平均値の分布のSD=\frac{標本集団データの分布のSD}{\sqrt{標本集団のデータ数}}$$
SEは「平均値の分布のSD(=平均値の分布のバラつき)」ですから、「どれだけ平均値を精度よく求められているか?」を表していると考えることができます。データ数を増やすとSEは小さくなっていきますので、精度が上がっていきます。例えばSEを半分にしたければ、データ数を4倍にすればよいです。
SDとSEの使い分け
SDとSEの使い分けが分からない、SDよりもSEの方が小さくて好ましいからSEを示すという声をよく聞きます。しかし、SDとSEの違いが分かれば、使い分けは明らかで、下表の通りです。
| 目的がデータの記述 | SDを用いる |
| 目的が平均値の精度を示すこと | SEを用いる |
なお、臨床研究では通常SEを用いずに信頼区間を用います。詳しくはp値と信頼区間の計算の記事で説明します。
標本集団から母集団の特徴を調べる
1つ前の記事で、「正規分布は平均値とSDが決まれば形が決まる」と述べました。正確には、「正規分布は平均値が決まると位置が決まり、SDが決まれば山の形が決まる」です。母集団データの分布が何であれ、平均値の分布は標本集団のデータ数が増えると正規分布に近づくため、SEを計算できれば、平均値の分布の山の形が決まります。それを基にしてp値や信頼区間を計算することができます(p値の概念はこちら、信頼区間の概念はこちらを参照)。このために正規分布は統計学において最重要と言われています。
神様になって、平均値の分布は標本集団のデータ数が増えると正規分布に近づくことが分かりましたので、神様でない人も、この性質は使うことができます。また、標本集団データの分布のSDから平均値のSEを計算できるので、ここでも神様になる必要はありません。
以上から、神様でない人も、標本集団から母集団の特徴を調べる術を手に入れることができました。
実際に標本集団から母集団の特徴をどう調べるかについては、p値と信頼区間の計算の記事で説明します。
まとめ
「正規分布とは?」の2つの記事で、下記を説明しました。なお、分布の要約(記述統計)については1つ前の記事のまとめをご覧ください。
- 正規分布は便利な特徴を持った分布である
- 母集団データの分布が何であれ、平均値の分布は標本集団のデータ数が増えると正規分布に近づく
- 平均値のSEは平均値の精度を表しており、標本集団データの分布のSDから計算できる
- 平均値のSEはデータ数を増やすと小さくなる
補足1: 統計量
標本集団から計算されるものを統計量と言います。今まで話をしてきた平均値も統計量の1つですし、例えば中央値や死亡割合も統計量の1つです。今までは「平均値の分布のSD=SE」と説明してきましたが、実際には「統計量の分布のSD=SE」です。統計量ごとにSEの式は違うのですが、ひとまず基本的な平均値のSEを理解していれば十分です。
補足2: 実際に用いられる分布
「母集団データの分布が何であれ、平均値の分布は標本集団のデータ数が増えると正規分布に近づく」と述べました。しかし、データ数が少ない場合はどうするのか?という問題や、「母集団データの分布のSDを標本集団データのSDで置き換えている」という問題があります。
そのため、実際には平均値の分布(正確には検定統計量の分布)としてt分布というものを使うことが多いですが、ここでは用語を含めて説明を割愛し、各検定の説明の際に詳しく説明します。
統計の多くの概念は正規分布を使うとイメージしやすく、また正規分布以外の分布を使う場合も同様のイメージで考えることができます。
イメージを持った上で細部に入れば、より理解を深めることが可能となります。現時点では細かいことは置いておいて、イメージを自分の中に形成することを重視してください。
