信頼区間とは?
本記事では信頼区間について説明します。なお、この記事は検定を理解していることを前提としているので、検定の考え方・有意水準とp値をまずはお読みください。
さて、この信頼区間も理解が困難な統計概念です。〇〇%信頼区間の定義は、「何度も同様の研究を行った場合に、その〇〇%は母集団の真の値(真の平均値等)を含むように構成された区間」です。
はい、もう分かりませんね…自分も初学者の頃は「何を言っているんだ?」という思いでした。しかし、実は検定を正しく理解していれば、そこから信頼区間を解釈することが可能です。以下でそれを説明します。
信頼区間と検定には密接な繋がりがある
検定では、証明したいことの逆(帰無仮説)を仮定して、そこで矛盾が起こったから帰無仮説を否定するという考え方をすると述べました。そして、臨床研究では、通常「全く効果なし(例えば平均値の差=0)」を帰無仮説として、そこでp値を計算すると述べました。この場合、「平均値の差=0」は否定され、「平均値の差は0ではない(平均値の差=0の逆、つまり、効果はある)」が正しいと判断します。
実は、この帰無仮説は「全く効果なし(平均値の差=0)」以外を設定できるのです(例えば「平均値の差=1とか平均値の差=5」等)。p値は設定した仮説の下で計算できます(p値の計算方法は別記事とします。ここでは考え方を示しています)。そうすると、「平均値の差=A」、「平均値の差=B」等、色々な帰無仮説に対して検定を行ってp値を計算でき、それぞれ帰無仮説が否定されると「平均値の差はAではない」、「平均値の差はBではない」となります。これを繰り返すと、「統計学的に有意とならない仮説の値の集まり」ができます。実は、これが信頼区間なのです。有意水準5%の検定を行うとすると、それに対応するのは95%(=100-5)信頼区間です。下図では、●が平均値、横棒が95%信頼区間です。
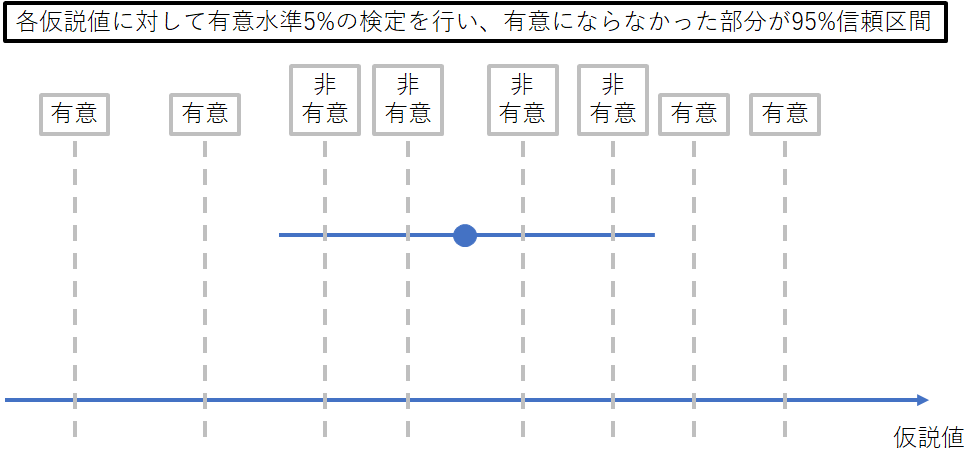
信頼区間の解釈
最初に述べた信頼区間の定義では、「じゃあ実際に得られた信頼区間はどう解釈すればいいの?」という問いに答えられません。一方、検定と結び付けた信頼区間は解釈できます。「統計学的に有意」というのは、帰無仮説の下で矛盾が得られたということです。「統計学的に有意とならない」ということは、帰無仮説の下で矛盾が示されなかった(帰無仮説の下で起こりにくいことではない)ということです。すなわち、信頼区間の解釈は、「検定で統計学的に有意とならなかった仮説値の範囲」→「データから矛盾判定されなかった仮説値の範囲」ということになります。
信頼区間 = データから矛盾判定されなかった仮説値の範囲
ここで、矛盾判定について下表にまとめました。
| 矛盾判定区分 | 説明 |
|---|---|
| 検定で矛盾判定された | データからは「母集団の真の値ではない」と判断されたという意味 |
| 検定で矛盾判定されなかった | データからは「母集団の真の値かどうかは不明(判断保留状態)」という意味 |
すなわち、「母集団の真の値かどうか不明な判断保留状態の区間」が信頼区間です。信頼区間の外は「母集団の真の値ではない」と判断されましたから、真の値は信頼区間のどこかにあると考えられます。なお、信頼区間の幅は患者数を増やすと狭くなっていきますが、これは人間の直感とも一致すると思います。すなわち、患者数を増やすと、判断保留状態の区間を狭めることができます。
このように作られた信頼区間、例えば95%信頼区間は、100回同様の研究を行った場合に、95個の95%信頼区間は母集団の真の値を含み、5個の95%信頼区間は真の値を含みません。これが最初に述べた信頼区間の定義ですが、解釈しにくいため、上記のような解釈をした方がよいです。これについて、補足を本記事の最後に記載しています。
さて、これらの解釈ができると、実は信頼区間はp値よりもずっと多くの情報を持っていて、かつp値で言えることは信頼区間で言えるのです。一般的に、「全く効果なし」というのは下表のとおりです。
| 見たいもの | 全く効果なしの仮説値 | 説明 |
|---|---|---|
| 差 | 0 | 95%信頼区間が0をまたがなければ、有意水準5%の検定で有意(p<0.05) |
| 比 | 1 | 95%信頼区間が1をまたがなければ、有意水準5%の検定で有意(p<0.05) |
そして、「統計学的に有意であることは臨床的に意味がある結果を意味しない」ということも分かります。例として、降圧薬A、B、Cの効果をプラセボと比較する研究A、B、Cを考えます。研究の開始後と開始前の収縮期血圧の変化量(開始後-開始前)をみます。それぞれの薬剤で変化量の平均値を出し、その変化量の平均値の差をとります(降圧薬-プラセボ)。なお、降圧薬は血圧を下げる薬ですので、変化量がマイナスであるほど血圧を下げる効果が高いということになります。血圧の単位はmmHgです。下図をご覧ください。下図はいくつかの研究の結果で、●が平均値、横棒が95%信頼区間です。なお、平均値の差がマイナスであるほど、降圧薬の降圧効果は高いことになります(下図では左に行くほどマイナスです)。
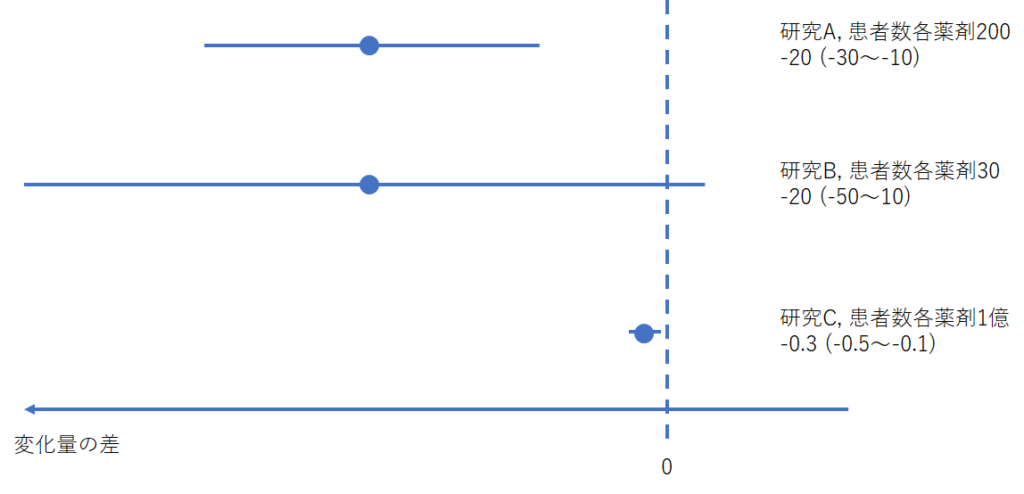
これらの研究の解釈は下記となります。95%信頼区間はデータから矛盾判定されない仮説値です。
| 研究 | 平均値 (95%信頼区間) | 臨床的意義 | 説明 |
|---|---|---|---|
| A | -20 (-30~-10) | あり |
|
| B | -20 (-50~10) | あり |
|
| C | -0.3 (-0.5~-0.1) | なし |
|
以上の結果から、「統計学的に有意であることは臨床的に意味がある結果を意味しない」ことが分かると思います(研究C)。また、「統計学的に有意でないからと言って、その後の研究を行う価値がない訳ではない」ということも分かります(研究B)。
臨床研究には制約がある
臨床研究において、患者数は有限であり、かつ「効果があるかどうかを証明するために研究している」のですから、場合によっては新規治療が有害という可能性もあります。そのため、臨床研究には倫理的な制約が常にあり、患者数を増やせばいいというものではありません(もちろん、研究費の問題もあります)。これらの制約を考慮した上で、「想定している位の効果があるならきちんと統計学的有意差が出るようにして、全く効果がないなら統計学的に有意とならないようにしよう」という考えが、臨床研究におけるサンプルサイズ設定です(サンプルサイズとは患者数と考えて構いません)。全く効果がない時に統計学的に有意となる確率をαエラー、想定している効果がある時に統計学的に有意とならない確率をβエラーと言います。また、想定している効果がある時に統計学的に有意となる確率(100-βエラー)を検出力(又はパワー)と言います。サンプルサイズ設定については別記事とします。目的を達成するために患者数を最小にすることは、倫理的にもコスト面でも非常に重要なことです。
これで信頼区間の説明は終わりです。「p値ではなく信頼区間を示すべき」という意見があり、これには私も賛成です。しかし、信頼区間と検定は密接に結びついていますから、「p値は誤用されるから信頼区間を示すべき」と言うのは意味がありません。統計的概念について正しい理解をした上で、結果を解釈することが重要です。
※信頼区間の補足
95%信頼区間を例に考えます。「得られた95%信頼区間に母集団の真の値が含まれる確率は95%である」は間違いだと専門家は言います。これについて補足します。
100回同様の研究を行った場合に、95個の95%信頼区間は母集団の真の値を含み、5個の95%信頼区間は真の値を含みません。個々の95%信頼区間が真の値を含んでいるか否かは確定しているため、「得られた95%信頼区間に母集団の真の値が含まれる確率は95%である」は間違いです。何故なら、母集団の真の値とは固定された1つの値だからです。
しかし、「100回同様の研究を行った場合に、95個の95%信頼区間は母集団の真の値を含み、5個の95%信頼区間は真の値を含まない」ということは、「得られた95%信頼区間に真の値が含まれていると考えてよいだろう」ということです。この「考えてよいだろう」という確信度のようなものを「95%の確率」と表現しているのであれば、それは解釈上問題ないと個人的には考えます。
