正規分布とは?その1(分布について)
統計学を学ぶ時に必ず出てくるものが正規分布です。本記事と次の記事で、正規分布と標準偏差・標準誤差について説明します。なお、標準偏差はStandard DeviationでSD、標準誤差はStandard ErrorでSEと略します。
さて、正規分布を説明する前に、まずはこの現実世界を見てみましょう。現実世界では、「絶対に〇〇だ/絶対に〇〇じゃない」ということはほぼありません。すなわち、ほぼ全てのデータがバラついています。バラつくというのは、「全てのデータが同じ結果にはならない」という意味です。例えば下表のように、至る所にバラついたデータは存在します。なお、データというのは数値だけではなく、食の好みのように、現実世界に存在するもの(考え方や思想等、抽象的なものも含む)は全てデータと考えることができます。
| データの種類 | 詳細 |
|---|---|
| 食の好み | Aさんは中華、Bさんはフレンチ、Cさんは日本食 |
| テストの点数 | Aさんは10点、Bさんは95点、Cさんは50点 |
| 薬剤投与の結果 | Aさんは病気が完治、Bさんは治らず死亡、Cさんはほぼ完治 |
統計学はバラついたデータを扱う学問です。バラついた個々のデータを見ただけでは、データの特徴や傾向は分かりにくいです。そのため、データを何らかの形で要約して、データの特徴や傾向を見やすくする必要があります。要約の方法としては大きく下記の2つがあります。
- 数値として要約する
- 平均値や中央値、SD
- 図として要約する
- ヒストグラムや箱ひげ図(箱ひげ図は説明しません)
分布の要約
まず、「分布」とは何でしょうか?分布とは「データがどのような頻度で存在しているか?」ということです。最もイメージしやすいのはヒストグラムです。下図は厚生労働省の平成21年国民生活基礎調査で示されている日本の世帯所得分布を示したヒストグラムです。
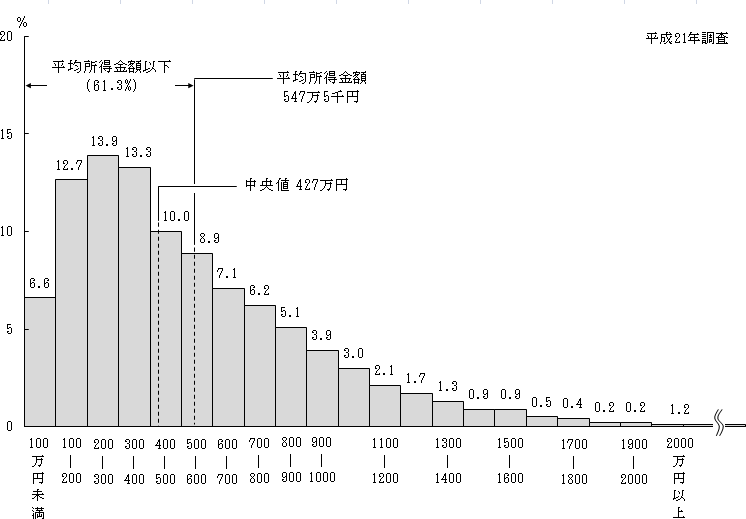
例えば、世帯所得が100万円未満の世帯は全体の6.6%、100-200万円(100万円以上200万円未満)は12.7%、というように、日本の世帯所得分布(世帯所得がどのような頻度で存在しているか)が視覚化されています。平均値は547万5千円、中央値は427万円となっています。平均値と中央値については下表に示しました。なお、世帯所得の例では、データは各世帯の所得です。
| 計算方法 | |
|---|---|
| 平均値 | データを全部足し合わせて、データの数で割る |
| 中央値 | データの真ん中の値(真ん中がない場合は、真ん中に近い2つを足して2で割る) |
世帯所得の図を見ると、左右対称の図ではなく、右に伸びた非対称な分布となっています。左右対称の分布では、平均値と中央値は一致するため、平均値は真ん中の値と解釈できます。しかし、右に伸びた分布の場合、平均値は中央値より大きな値となります。平均値は547万5千円ですが、実際には半分の世帯が427万円以下の所得です。このような左右非対称の分布では、真ん中の値を知りたい場合、平均値ではなく中央値を使用するべきです。
正規分布
先ほど世帯所得の分布を見ましたが、左右非対称で右に伸びた分布でしたね。統計学では、何か便利な特徴を持った分布には特別な名前がついています。正規分布、二項分布、一様分布、等です。統計学において最重要は正規分布です。下図はいくつかの正規分布を図示したものです。なお、点線は平均値=0、SD=1の正規分布を比較のために重ね合わせたものです(SDは下で説明しています)。とても滑らかな分布ですが、イメージとしては、先ほど示したような「ヒストグラムを滑らかに結んだもの」と考えてよいです(本記事の後半に重ね合わせた図を示しています)。
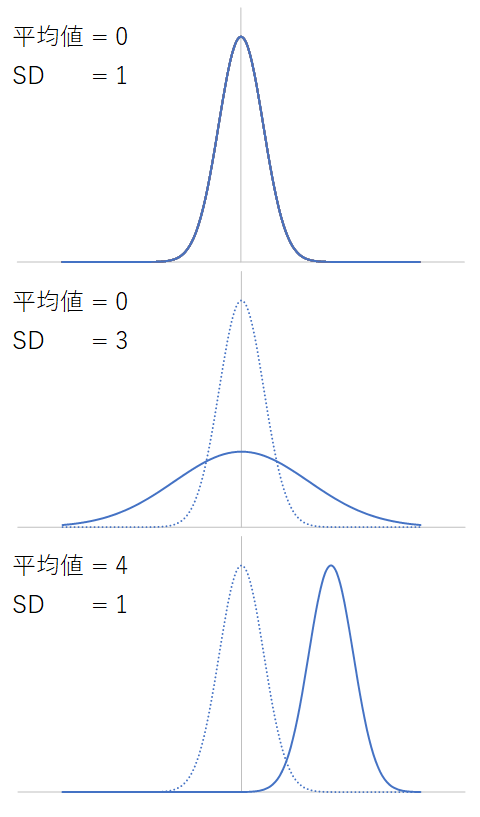
便利な特徴を持った分布には特別な名前がついていると先ほど述べましたが、正規分布には以下のような特徴があります。
- 左右対称で山が1つである
- 平均値とSDが決まれば形が決まる
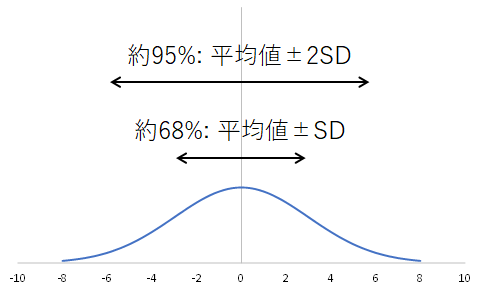
- 平均値±SDの範囲に約68%のデータがある
- 平均値±2SDの範囲に約95%のデータがある
- 次の記事で述べる特徴がある(今は知らなくて結構です)
「正規分布って何?」という質問の答えは、「上のような特徴を持った分布」です。特徴の2の「平均値とSDが決まれば形が決まる」というのは、先ほどの図を見ると分かります。下表のようになります。
| 平均値が変わる |
|
| SDが変わる |
|
さて、SDについてですが、私はSDの計算式を知る必要はないと思っているので、ここでSDの式は示しません(気になる方はググってください。なお、不偏分散が使われている方を見てください)。なぜかというと、数式を見てもいまいちSDの解釈は分からず、また正規分布以外ではSDは解釈しにくいためです。
SDは「どれだけバラついているか(分布の山がどれだけなだらかか/鋭いか)」を表すものと考えればよいのですが、特徴の3と4のイメージができていれば十分です。
数値での分布の要約
さて、正規分布のこれらの特徴を知っていれば、実は「平均値±SDで数値として分布が要約できる」ということが分かります。なぜなら、特徴の2で正規分布の形は平均値とSDで決まりますし、特徴の3で平均値±SDの範囲にデータの約68%があると分かるからです。一般的な医学論文の「背景項目の要約」では数値表として要約されており、例えば下表のようにまとめられます。
| 項目 | 薬剤A (人数=51人) | 薬剤B (人数=49人) |
|---|---|---|
| 年齢 (歳), 平均値±SD | 45.0±5.1 | 44.7±5.2 |
| 診断されてからの年数 (年), 中央値 (最小値~最大値) | 10 (2~30) | 12 (2~31) |
このように数値表を用いることで、大まかに薬剤Aと薬剤Bの人たちの背景が似通っているかどうかを確認することができます。一般的に背景項目はいくつもあり、全てを図示して論文に載せることは現実的ではないため、数値表を用います。
まとめるルールは下記になります。なお、「ほぼ」や「大きく」というのは主観的な表現ですが、「この程度ならこの要約方法」という明確な基準はありません。ただし、平均値±SDがおかしな範囲になる場合は中央値 (最小値~最大値)で要約します。例えば、0以上の値しか取らない検査値なのに、平均値-SDがマイナスになる場合等です。完全な左右対称は数学の世界にしかありません。例えば先ほどの世帯所得の分布を見れば、「これはほぼ左右対称とは言えないでしょ」と多くの人が考えると思います。
| ほぼ左右対称で山が1つである分布 | 平均値±SD |
| 大きく左右非対称かデコボコした分布 | 中央値 (最小値~最大値) |
最小値~最大値は25%点~75%点というものを用いることもありますが、ここでは割愛します(「パーセント点 中央値」等でググってみてください)。
面積と割合
統計学を学んでいると、至る所で「分布の下側の面積」を割合と考えている図を見かけますし、このブログでもそのような図は出していきます。下記でそれを理解するための説明をします。
先ほどヒストグラムを見ました。ヒストグラムを滑らかに線で結んだものとヒストグラムを下記に示しています。

データがたくさんあれば、ヒストグラムの幅をドンドン狭められます。ヒストグラムの幅を狭めていけば、ヒストグラムはどんどん滑らかになっていきます。そうすると、上図の一番右のように、滑らかな線の下部分の面積はヒストグラムを足し合わせたものと等しくなっていきます。例えば、身長が170cm以上の人の割合は、黄色部分の面積で表せます。今後、「分布の下側の面積が割合」と表現している図があれば、この説明をイメージしてください。
ここまでのまとめ
本記事では、現実世界のデータはバラつくこと、バラつくデータは要約して見やすくすることを述べました。次に、分布とは「データがどのような頻度で存在しているか?」ということ、それをイメージするものとしてヒストグラムを示しました。また、正規分布の特徴とSDの解釈、数値としての要約方法を述べ、分布の下側の面積が割合を表すことを説明しました。
これらは今後の色々な概念の説明を理解するための基礎となるので、是非イメージで理解してください。
