p値の計算
「検定の考え方・有意水準とp値」では、検定の考え方、有意水準とp値の解釈について述べました。検定は下記の手順で実施しますが、本記事ではこのうち3番目の「p値を計算する」考え方について説明します。
- 帰無仮説を設定する
- 起こりにくさの基準である有意水準を決める(通常、両側5%または片側2.5%)
- p値を計算する
- p値≦有意水準であれば、帰無仮説が間違っていると判断する。
なお、ここでは平均値に注目している場合で考えます。
平均値の分布
「正規分布とは?その2(標準誤差について)」では、下記を説明しました。
- 平均値もバラつくこと(平均値の分布を考えることができること)
- 平均値の分布のバラつきを標準誤差(SE)と言い、SEはデータのバラつきである標準偏差(SD)から計算できること
- 平均値の分布はデータの数が増えると正規分布に近づくこと
また、「正規分布とは?その1(分布について)」では、下記を説明しました。
- 正規分布は平均値とバラつきが決まれば形が決まること
- 分布はヒストグラムのイメージで、滑らかな分布の下側の面積は全体に対する割合を表す
p値の正確な定義は、「検定の考え方・有意水準とp値」にも記載しましたが、「得られた結果かそれ以上に極端な結果が帰無仮説の下で起こる確率(割合)」です。
さて、ここで、収縮期血圧を下げると考えられる開発中の薬Xがあり、Xの服薬前に比べて、Xの服薬12週後の血圧が下がるかどうかを調べたいとします。実際の研究では効果のないプラセボを服薬する人たちを設定したりもしますが、ここでは簡単のために薬Xを服薬する人たちのみとします。研究終了後、収縮期血圧の差(12週後の血圧-服薬前の血圧)を参加者ごとに求め、収縮期血圧の差の平均値を出します。
ここで、帰無仮説として「差の平均値=0」だと考えてみましょう。これは、「真実(母集団の差の平均値)は0なんだ」と考えているということです。有意水準は5%とします。9名の方が研究に参加し、実際の血圧の差として下記が得られたとします。
-41, -43, 10, 15, -30, -26, -34, -10, 15
得られた平均値は-16、標準偏差は24、標準誤差は8です。
今、「真実(母集団の差の平均値)は0なんだ」という帰無仮説が正しいと考えていますから、平均値の分布の平均値は0です。そして、平均値の分布のバラつきは標準誤差なので、データから計算した8です。正規分布は平均値とバラつきが決まると形が決まります。これらから、p値は下図の黄色部分の面積となります。
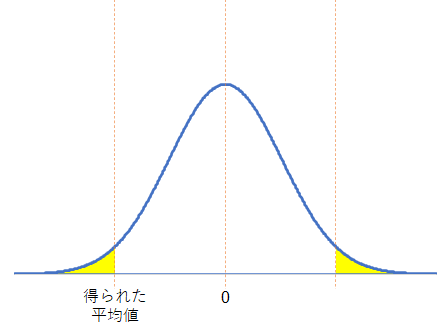
p値の定義「得られた結果かそれ以上に極端な結果が帰無仮説の下で起こる確率」の「それ以上に極端な」というのは、「真実から離れる方向の結果」という意味です。得られた差の平均値は-16ですから、「差の平均値として-16以下の部分」が上図の左側の黄色部分に該当します。また、真実を挟んで反対側以上の部分も通常p値に含めるので、「差の平均値として16以上の部分」(上図の右側の黄色部分)も計算します。正規分布の場合は左右対称なので、左側部分×2でp値が計算でき、p値は0.0455となります。0.0455<0.05なので、p値が有意水準以下となり、帰無仮説は間違っていると判断します。
なお、エクセルで上記の黄色部分を計算する場合、下記の式で計算することができます。
=NORM.DIST(-16, 0, 8, TRUE) * 2
まとめ
本記事ではp値の計算の考え方について示しました。
- 帰無仮説の下での平均値の分布を考える(真実は帰無仮説の値で、標準誤差はデータから計算)
- 平均値の分布に対して、得られた平均値が帰無仮説からどれだけ乖離しているかを見ている
実際にはp値は統計ソフトが自動的に計算してくれます。
また、ここでは平均値に注目しましたが、考え方は平均値に注目しない場合でも同様です。その場合、考える分布が正規分布ではないこともありますが、その点については個々の検定を説明する際に説明したいと思います。
補足1
「標準誤差はデータから計算できる」と言いましたが、素直に考えると、この標準誤差はデータが変わると変わります。
「正規分布とは?その2(標準誤差について)」の補足2でも述べましたが、実際には「標準誤差をデータから求めている」ということを考慮し、平均値の分布(正確には検定統計量の分布)としてt分布を用います。この場合の検定をt検定と言います。これは、統計の本では「分散が未知の場合」と説明されています。
一方、本記事で計算したのは、得られた標準誤差が真実だと考えたものになりますが、この場合の検定をz検定と言います。これは、統計の本では「分散が既知の場合」と説明されています。
なお、本記事の例をt検定を用いてp値を計算した場合、0.0805>0.05となり、統計学的に有意ではなくなります。このように、検定で仮定していることによってp値は変わりますので、適切な検定を選択する必要があります。このt検定のp値はエクセルで下記で算出できます。
=T.DIST((-16-0)/8, 9-1, TRUE) * 2
